Practical physics in a time of pandemic
http://bit.ly/Practicalsinatimeofpandemic081020
Spark.iop.org: https://spark.iop.org/search?query=remote%20teaching
A diagram of two people Description automatically generated with medium confidence
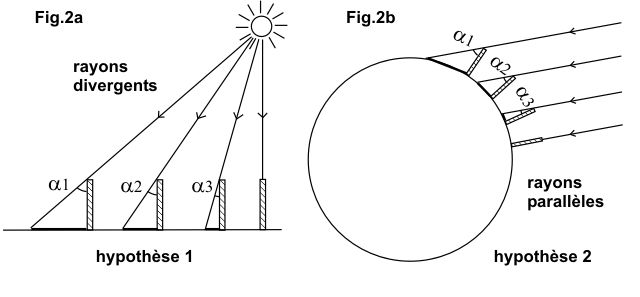
Eratosthenes did his experiment by taking measurements in two locations: Alexandria and Syene. But we can easily modify his experiment by making measurements in three or more places, and the flat-Earth model is instantly proven wrong.
A diagram of a solar system Description automatically generated
Picture courtesy of Eratosthenes.eu
Using the flat-Earth model, the length of the shadow will have a linear response. On the other hand, using the spherical Earth model, the length of the shadow has a non-linear response.
We can also observe that in near-polar locations, the experiment will result in a very long shadow. The flat-Earth model cannot explain this phenomenon.
Furthermore, the flat-Earth model will not produce a consistent result. It is not a coincidence that not a single flat-Earther can give us the exact distance to the Sun. Their outcome will vary a lot even though this experiment does not demand high precision and accuracy.
How to do it:
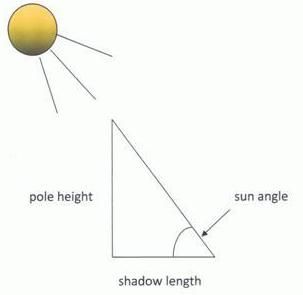
First, calculate your local noon because it may be quite different from 12:00 noon on the clock. There are several ways to compute its exact occurrence. Basically, local noon is half-way between sunrise and sunset. You can obtain sunrise and sunset times, for June 21, from your local paper or from this link: http://aa.usno.navy.mil… which also calculates local noon (sun transit). You can also obtain it by yourself by using a sundial or find out when the shadow is the shortest around noon time.
On June 21 erect a vertical straight stick or pole of about 1 meter using a carpenter’s level and measure the length of the shadow it casts at your local noon. With simple trigonometry you can obtain the angle of the elevation of the sun. You can also obtain the angle, without trigonometry, by drawing the stick and shadow proportionally and measuring it with a protractor. You can compare your results with a web based applet like this: http://www.jgiesen.de/azimuth but be careful to use it correctly (insert your correct time zone, local noon, coordinates, date and ensure that the dropdown menu points to elevation).
 Sun
Elevation Angle |
|---|
After you get the angle of sun elevation, it’s very easy to calculate the zenith angle by subtracting it from 90°, like Eratosthenes did. Now you’ll have to measure the distance from your location to the Tropic of Cancer latitude line - not by camel caravans of course, the Eratosthenes way. You can use a relatively large scale map, but take in account that maps tend to distort distance and the best option is to use a globe. The distance from your location to the Tropic of Cancer should be measured from north to south. In other words the distance line has to cut the Tropic of Cancer at a right angle. There are also web based calculators for this: https://web.archive.org….
Now it’s easy to calculate the Earth circumference by using the following formula:
Earth Circumference
Formula
Likewise, you can also perform this experiment on the winter solstice that takes place around 21 December, but you’ll have to measure your distance from the Tropic of Capricorn instead from the Tropic of Cancer because on this date the sun reaches its highest degree of elevation on the Tropic of Capricorn (23° 26′ 22″ south of the Equator).
It is also possible to perform this experiment on the two Equinoxes which occur on 20 March and 23 September each year when the sun is crossing the equator at the local noon on those dates and the sun rays are just overhead the equator at a right angle to the ground. But instead to measure your distance from the Tropic of Cancer or the Tropic of Capricorn you’ll have to measure it from the equator.
There is another option and you can perform this experiment on any other date of the year, at local noon time, but you should have some partner located on your longitude willing to measure sun elevation at the same time. Take in account that you’ll have to be a little careful treating correctly the sun angles obtained in this case.
At any date the sun reaches its highest position, at noon time, at some latitude. From here is clear that if the two places involved are located on the same side of this latitude (north or south) the shadows will be casted at the same direction and the obtained angles should be subtracted from each other, whereas if the places are located on different sides of this latitude the shadows will be casted at different directions (southward or northward) and the angles should be added up.
In case of a cloudy weather please follow the instructions here on how to get a measurement of the Earth’s circumference
http://www.eso.org/public//outreach/eduoff/aol/market/collaboration/erathostenes/