JRowing
Interesting Graphs Experiments CPD Sessions Intro to A-level Practicals Photos Experiment results Multiple choice physics questions Excel Sims Education Theory Seismic

Archives Search Feed Twitter --- Buy me a coffee About
 

An introduction to…Specific Heat and Mechanical Equivalent of Heat

James Joule (1818-1889) was the first to establish by experiment that heat and mechanical work are both forms of energy and that they can be quantitatively related to one another. The purposes of this experiment are (I) to measure the specific heat of a substance, i.e., to determine the amount of heat that must be applied to a unit mass of substance in order to change its temperature by one degree, and (II) to determine by experiment the relationship between the “heat” energy units (MKS - kilocalorie, or British - BTU) and the “mechanical” energy units (MKS - Joule, or British - footpound).

Part I - Specific Heat

Physical Principles

The amount of heat required to raise the temperature of a unit mass of a substance by one degree is called the specific heat of that substance. Thus, if an amount of heat Q is added to a substance of mass m having a specific heat c, the change in temperature ∆T = Tf − Ti will be given by

Q

∆T = or Q = mc∆T

mc

In the MKS system, the unit of heat is the kilocalorie and is defined so that the specific heat of water is one–i.e., when one kilocalorie of heat is applied to one kilogram of water, its temperature will rise by one degree Centigrade (Celsius).

When two or more substances at different temperatures are brought together, they will come into thermal equilibrium after a short period of time because heat will flow from the warmer to the cooler substance until all materials are at the same temperature. If the materials which make up the system of interest are insulated so that no heat can be transferred to or from the surroundings, the process is said to be adiabatic. Since heat is a form of energy, the law of conservation of energy requires that for an adiabatic process the sum of all the heat transfers among parts of the system must be equal to zero. Note: If heat is added to a substance, then Tf > Ti and Q is positive; if heat is removed, then Tf < Ti and Q is negative.

In this part of the experiment, a mass mL of lead will be heated to a temperature TL. The hot lead will be placed in a mass mW of water at a known temperature TW . If TW < TL, heat will flow from the lead into the water until the equilibrium temperature Te is reached. Then the sum of the heat transfers will equal zero.

QL = mLcL (Te −TL )

= mWcW (Te QL +QW = 0 QW −TW )

If the values of temperature and mass are known, the specific heat cL of lead can be determined.

Experimental Apparatus

The experimental apparatus consists of the following items:

  1. A block of lead, held by a string.

  2. An electrically heated kettle, in which you can bring water to a boil and then, putting the block of lead into the boiling water, heat the lead to the same temperature. (Do not fill the kettle more than 2/3 full.)

  3. A “Styrofoam” container of negligible mass which serves as a well-cup for allowing a small amount of cool water and the hot block of lead to come to thermal equilibrium. (Put a paper cup inside the Styrofoam cube before adding water. Do not put water directly into the cube.)

  4. A thermometer for measuring the temperature of the water in the container.

  5. A balance for weighing the water and the lead.

Procedure

  1. Use the above equipment to measure cL for two blocks of lead.

  2. Compare your result with the accepted value for the specific heat of lead,

KCal

cL = 0.031

Kg deg C

and comment on sources of error in the experiment.

  1. Why is it advisable to start with water which is a few degrees below room temperature?

  2. It is recommended that you stir gently to assure uniform temperature in the water. Does stirring introduce a significant source of error?

CAUTION: UNPLUG THE WATER HEATER WHEN YOU ARE DONE, EMPTY ALL THE WATER OUT AND LEAVE THE HEATER DISCONNECTED.


Part II - Mechanical Equivalent of Heat

Physical Principles

When an object starts with zero initial velocity and falls through a distance h, its initial potential energy mgh is converted into kinetic energy as it falls. When the object comes to rest after impact at the bottom of the fall, the kinetic energy is converted into the energy of molecular vibrations (heat). This fact is apparent from the observable rise in the object’s temperature after the fall. When the specific heat and the mass of the object are known, the amount of heat added to the object during impact can be determined from the change in temperature. If you are sure that all of the original mechanical energy was transformed into heat energy and that a negligible amount of heat escaped from the object, you can determine the relationship between the units used for mechanical energy and the units used for heat energy. This conversion constant is called the mechanical equivalent of heat, J.

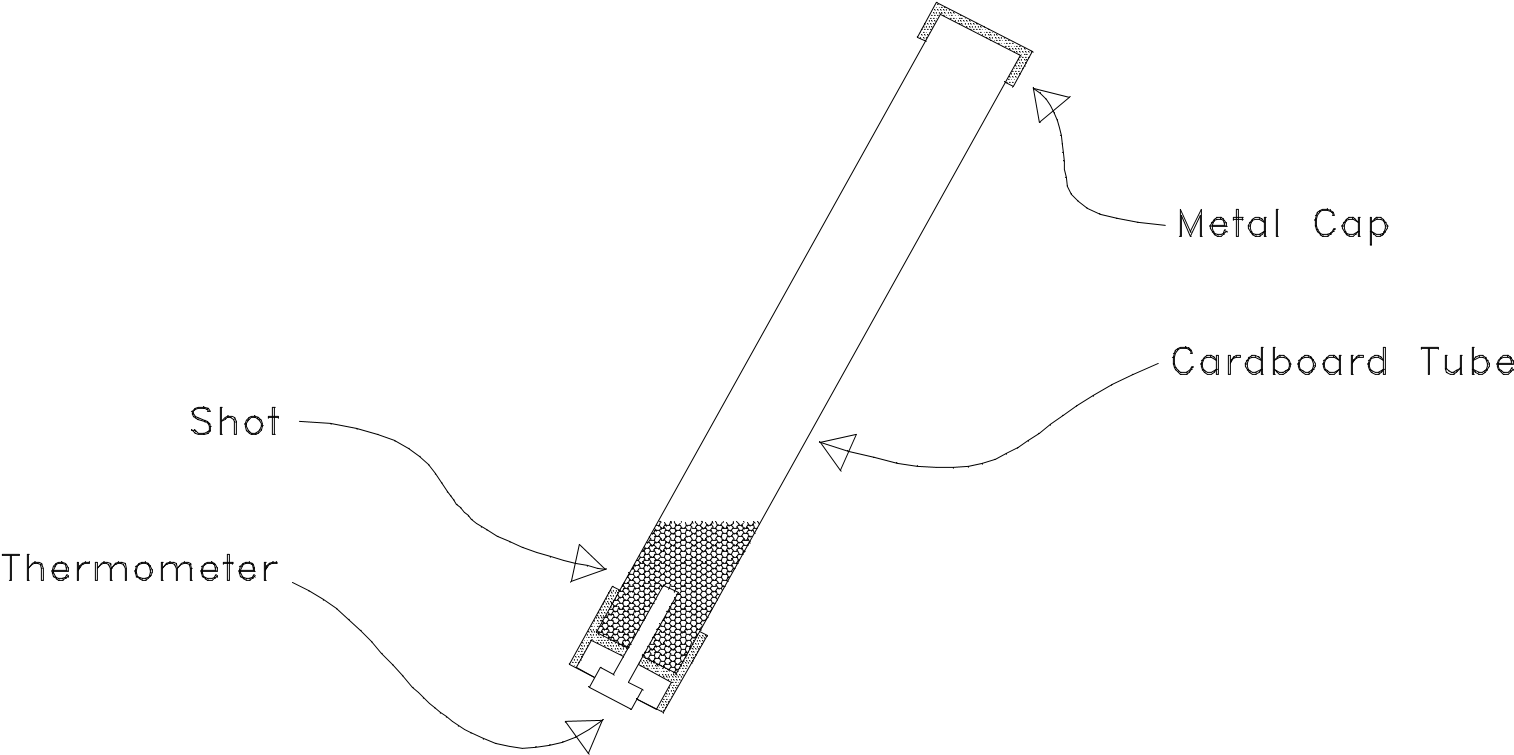
In this experiment, about 1 kg of lead “shot” (small pellets) has been placed in a cardboard tube about one meter long, which is permanently closed at both ends, with a metal dial thermometer mounted in one end. The cardboard is an extremely poor conductor and has a low heat capacity. Thus, when the shot is made to fall vertically from one end of the tube to the other a large number of times, most of the heat developed is absorbed by the shot itself, while an insignificant portion is taken up by the cardboard and the light thermometer stem.

The mechanical equivalent of heat can be determined by measuring h, the total distance through which the shot has fallen, and ∆T, the temperature rise of the shot, and by using the value of the specific heat of lead measured in Part I.

CAUTION: DO NOT ATTEMPT TO REMOVE EITHER OF THE CAPS FROM THE CARDBOARD TUBE; THEY ARE MEANT TO BE PERMANENTLY SEALED.

(This prevents the spilling of any lead dust, which accumulates in the tube.)

Procedure

  1. Cool the lead shot 5-7 degrees below room temperature by placing the end of the cardboard tube for a few minutes in an empty metal pipe which is suspended in an ice bath. Do not get the tube wet!

  2. Agitate the shot very slightly to ensure thermal equilibrium. Allow the thermometer to remain in contact with the shot for 2-3 minutes before taking a reading.

  3. After thermal equilibrium has been established, record the temperature of the shot. It should be about 3-4 degrees below room temperature.

  4. Proceed to invert the tube N times (approximately 75) in rapid succession. When inverting the tube, place the lower end on the table so that the falling shot does not force out the ends. Try to keep your hands away from the ends of the tube since it is desirable that the ends should not be influenced by the heat of your hands.

  5. When you have completed the last inversion, repeat the procedure for recording the temperature of the shot. For best accuracy the temperature of the shot should be approximately as much above room temperature as it was below room temperature initially. Why? If this is not the case, you should discuss the error that this would introduce in your conclusion.

  6. Measure the total height h through which the center of mass of the shot has fallen. (Use the marks on the outside of the tube, which indicate the location of the shot at each end of the tube.)

  7. Using the value of the specific heat of lead measured in Part I, and the measured value of h and ∆T, calculate J, the mechanical equivalent of heat.

  8. Repeat the measurement, and compare the average value of J from your two trials with the accepted value of 4185 Joules/KCal. What are the major sources of error in your measurement?